NumPy and the ndarray#
Steven Pestana (spestana@uw.edu) (Adapted from the water data tutorials from Waterhackweek 2020)
By the end of this notebook you will be able to:
Create and manipulate ndarrays
Index and slice ndarrays
NumPy: working with multi-dimensional arrays in python#
The NumPy library is at the core of the “scientific python ecosystem”. NumPy provides an ndarray data type which can be used to represent multi-dimensional gridded data. It also includes linear algebra functions and other useful math functions.
See these resources for more detailed NumPy information and tutorials:
To get started, import NumPy and give it an alias np (this shorthand is commonly used in the python community)
import numpy as np
Creating arrays#
Take a quick look at the np.array() function that lets us create an array. The main input that this function needs is an “array_like” object. We can create a python list of integer values and pass it to this function to turn that list into an ndarray.
help(np.array)
Help on built-in function array in module numpy:
array(...)
array(object, dtype=None, *, copy=True, order='K', subok=False, ndmin=0,
like=None)
Create an array.
Parameters
----------
object : array_like
An array, any object exposing the array interface, an object whose
__array__ method returns an array, or any (nested) sequence.
dtype : data-type, optional
The desired data-type for the array. If not given, then the type will
be determined as the minimum type required to hold the objects in the
sequence.
copy : bool, optional
If true (default), then the object is copied. Otherwise, a copy will
only be made if __array__ returns a copy, if obj is a nested sequence,
or if a copy is needed to satisfy any of the other requirements
(`dtype`, `order`, etc.).
order : {'K', 'A', 'C', 'F'}, optional
Specify the memory layout of the array. If object is not an array, the
newly created array will be in C order (row major) unless 'F' is
specified, in which case it will be in Fortran order (column major).
If object is an array the following holds.
===== ========= ===================================================
order no copy copy=True
===== ========= ===================================================
'K' unchanged F & C order preserved, otherwise most similar order
'A' unchanged F order if input is F and not C, otherwise C order
'C' C order C order
'F' F order F order
===== ========= ===================================================
When ``copy=False`` and a copy is made for other reasons, the result is
the same as if ``copy=True``, with some exceptions for 'A', see the
Notes section. The default order is 'K'.
subok : bool, optional
If True, then sub-classes will be passed-through, otherwise
the returned array will be forced to be a base-class array (default).
ndmin : int, optional
Specifies the minimum number of dimensions that the resulting
array should have. Ones will be pre-pended to the shape as
needed to meet this requirement.
like : array_like
Reference object to allow the creation of arrays which are not
NumPy arrays. If an array-like passed in as ``like`` supports
the ``__array_function__`` protocol, the result will be defined
by it. In this case, it ensures the creation of an array object
compatible with that passed in via this argument.
.. versionadded:: 1.20.0
Returns
-------
out : ndarray
An array object satisfying the specified requirements.
See Also
--------
empty_like : Return an empty array with shape and type of input.
ones_like : Return an array of ones with shape and type of input.
zeros_like : Return an array of zeros with shape and type of input.
full_like : Return a new array with shape of input filled with value.
empty : Return a new uninitialized array.
ones : Return a new array setting values to one.
zeros : Return a new array setting values to zero.
full : Return a new array of given shape filled with value.
Notes
-----
When order is 'A' and `object` is an array in neither 'C' nor 'F' order,
and a copy is forced by a change in dtype, then the order of the result is
not necessarily 'C' as expected. This is likely a bug.
Examples
--------
>>> np.array([1, 2, 3])
array([1, 2, 3])
Upcasting:
>>> np.array([1, 2, 3.0])
array([ 1., 2., 3.])
More than one dimension:
>>> np.array([[1, 2], [3, 4]])
array([[1, 2],
[3, 4]])
Minimum dimensions 2:
>>> np.array([1, 2, 3], ndmin=2)
array([[1, 2, 3]])
Type provided:
>>> np.array([1, 2, 3], dtype=complex)
array([ 1.+0.j, 2.+0.j, 3.+0.j])
Data-type consisting of more than one element:
>>> x = np.array([(1,2),(3,4)],dtype=[('a','<i4'),('b','<i4')])
>>> x['a']
array([1, 3])
Creating an array from sub-classes:
>>> np.array(np.mat('1 2; 3 4'))
array([[1, 2],
[3, 4]])
>>> np.array(np.mat('1 2; 3 4'), subok=True)
matrix([[1, 2],
[3, 4]])
Create a 1-dimensional array from a list object:
my_list = [0,1,2,3,4,5,6,7,8,9]
# check the type of my_list
type(my_list)
list
# create an array from this list
one_dimensional_array = np.array(my_list)
print(one_dimensional_array)
[0 1 2 3 4 5 6 7 8 9]
We can check the data type of this object, and see that it is an ndarray
type(one_dimensional_array)
numpy.ndarray
We can also look at the array’s shape, and data type of its contents. Because we didn’t specify in the np.array() function what data type we wanted, it will by default pick a data type for us based on the values in the list object we provided.
one_dimensional_array.shape
(10,)
one_dimensional_array.dtype
dtype('int64')
Create a 2-dimensional array (this array has three rows and three columns):
two_dimensional_array = np.array([[1.44, 2.50, 3.72],
[1.98, 2.12, 3.89],
[1.04, 2.63, 3.17]])
print( two_dimensional_array )
print("\n Our array has a shape of {}".format( two_dimensional_array.shape ) )
[[1.44 2.5 3.72]
[1.98 2.12 3.89]
[1.04 2.63 3.17]]
Our array has a shape of (3, 3)
Check the data type of the array’s contents. Note that because we provided numbers with some fractional value, numpy chose a floating-point data type for us. We could have also specified this ourselves by including the argument dtype=np.float64 when we created the array.
two_dimensional_array.dtype
dtype('float64')
Create an array filled with zeros using np.zeros()
# create a 5 by 10 array of just zeros
array_of_zeros = np.zeros((5,10))
print("Array of zeros:\n{}".format(array_of_zeros))
Array of zeros:
[[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]]
Create an array filled with ones using np.ones()
# create a 1 dimensional array of just ones
array_of_ones = np.ones(10)
print("Array of ones:\n{}".format(array_of_ones))
Array of ones:
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]
Create an array filled with ones, with the same shape as another array, using np.ones_like() (also try np.zeros_like())
# create an array of ones with the same shape as our earlier 2D array:
array_of_ones_2d = np.ones_like(two_dimensional_array)
print("Array of ones like two_dimensional_array:\n{}".format(array_of_ones_2d))
Array of ones like two_dimensional_array:
[[1. 1. 1.]
[1. 1. 1.]
[1. 1. 1.]]
Create an empty array with np.empty(), then fill it with a specific value we want.
# create an empty array
my_array = np.empty(10)
# then fill it with some value
my_array.fill(3.14)
print("My array:\n{}".format(my_array))
My array:
[3.14 3.14 3.14 3.14 3.14 3.14 3.14 3.14 3.14 3.14]
Use np.arange() to get values spaced evenly within an interval.
# create an array with values between 1 and 100, incrementing by 5 with each step
my_arange_array = np.arange(1, 100, 5)
print("Array with values between 1 and 100, incrementing by 5 with each step:\n{}".format(my_arange_array))
Array with values between 1 and 100, incrementing by 5 with each step:
[ 1 6 11 16 21 26 31 36 41 46 51 56 61 66 71 76 81 86 91 96]
Use np.linspace() and np.logspace() to get linear and logarithmic arrays between an interval.
# create a linear array with values between 10 and 10000
my_linear_array = np.linspace(10, 10000, 4)
print("Linear array:\n{}".format(my_linear_array))
# create a logarithmic array with values between 10**1 and 10**4
my_log_array = np.logspace(1, 4, 4)
print("\nLogarithmic array:\n{}".format(my_log_array))
Linear array:
[ 10. 3340. 6670. 10000.]
Logarithmic array:
[ 10. 100. 1000. 10000.]
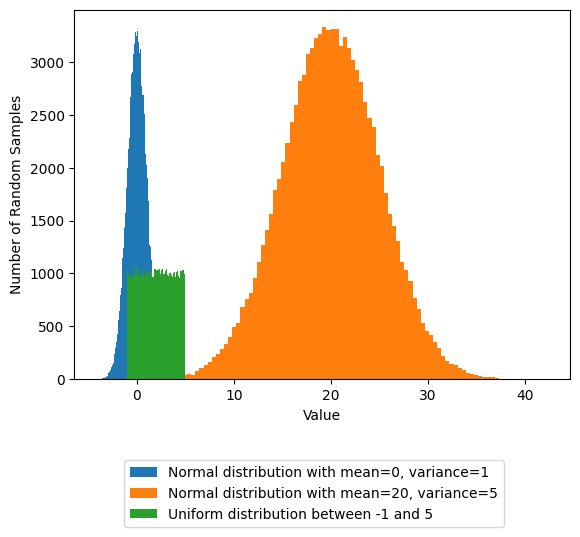
Finally, create arrays filled with \(10^5\) random numbers sampled from different distributions using np.random functions.
# create an array of 5 random samples from a normal distribution with mean=0, variance=1
my_random_array_1 = np.random.randn(10**5)
print("Random samples from a normal distribution with mean=0, variance=1:\n{}".format(my_random_array_1))
# create an array of 5 random samples from a normal distribution with mean=20, variance=5
my_random_array_2 = np.random.normal(20, 5, 10**5)
print("\nRandom samples from a normal distribution with mean=20, variance=5:\n{}".format(my_random_array_2))
# create an array of 5 random samples from a uniform distribution between -1 and 5
my_random_array_3 = np.random.uniform(-1, 5, 10**5)
print("\nRandom samples from a uniform distribution between -1 and 5:\n{}".format(my_random_array_3))
Random samples from a normal distribution with mean=0, variance=1:
[ 0.47846805 0.82451382 0.08843784 ... 0.09073678 -0.8703055
-0.40311245]
Random samples from a normal distribution with mean=20, variance=5:
[17.32958289 18.22103205 18.2498759 ... 22.25629205 17.75103256
8.89212444]
Random samples from a uniform distribution between -1 and 5:
[ 0.95415713 4.54324205 3.64987693 ... -0.4251362 1.26567284
1.95249604]
Import matplotlib and plot these random samples from different distributions:
import matplotlib.pyplot as plt
%matplotlib inline
plt.hist(my_random_array_1, bins=100, label='Normal distribution with mean=0, variance=1')
plt.hist(my_random_array_2, bins=100, label='Normal distribution with mean=20, variance=5')
plt.hist(my_random_array_3, bins=100, label='Uniform distribution between -1 and 5');
plt.xlabel('Value')
plt.ylabel('Number of Random Samples')
plt.legend(loc=(0.1,-0.4))
<matplotlib.legend.Legend at 0x7fc38833df50>
Index/slicing ndarrays#
To select specific elements within an ndarray, you can use slicing, or indexing.
The syntax for specifying a slice is x[i:j:k] where for an array x, i specifies the index to start the slice at, j the index to end the slice, and k the step size to take moving between i and j. A step size of 1 does not need to be explicitly stated, it is the default when no step size is provided (x[i:j]).
# Create a one dimensional array to work with
one_dimensional_array = np.arange(0,10,1)
# Print out our array
print("\n A one dimensional array:\n{}".format(one_dimensional_array) )
A one dimensional array:
[0 1 2 3 4 5 6 7 8 9]
Slicing an array: Starting at the first element (index=0), slice until the fifth element, with a step size of 2
# Starting at the first element (index=0), slice until the fifth element, with a step size of 2
one_dimensional_array[0:5:2]
array([0, 2, 4])
Negative indexes will count backwards from the last element in an array (where the last element has index of -1).
# Select the second-to-last element of this one-dimensional array
one_dimensional_array[-2]
8
We can use these methods to change the values in the array. To do this, we first specify the index we want to change, then assign a new value with =
one_dimensional_array[0] = 10
# Print out the array now that we've change one of its values
print("\n Our modified array:\n{}".format(one_dimensional_array) )
Our modified array:
[10 1 2 3 4 5 6 7 8 9]
And can perform all sorts of math functions on the entire array or segments of the array.
Note that here we’re using a shorthand syntax where x = x * 2 is equivalent to x *= 2 (similarly x = x + 1 is equivalent to x += 1)
# Multiply the first four values by two, and replace the original values with the new values
one_dimensional_array[0:4] *= 2
one_dimensional_array
array([20, 2, 4, 6, 4, 5, 6, 7, 8, 9])
We can also use conditional statements to create arrays of boolean values (True/False), and use these boolean arrays to select elements from an array.
# Find even numbers by taking modulo 2
even_number_conditional = one_dimensional_array % 2 == 0
print(even_number_conditional)
[ True True True True True False True False True False]
# Now use this to select only where our boolean array is True
one_dimensional_array[even_number_conditional]
array([20, 2, 4, 6, 4, 6, 8])
# We can use the "~" (bitwise not) operator to invert our boolean array values, and then select only odd numbers
print(~even_number_conditional)
one_dimensional_array[~even_number_conditional]
[False False False False False True False True False True]
array([5, 7, 9])
Working with more than one dimension#
We can slice through multiple dimensions, separating the slice for each dimension with a comma like x[i:j:k,l:m:n] where i, j, and k slice the first dimension, and l, m, and n slice the second dimension.
# Create a two dimensional array to work with
two_dimensional_array = np.random.normal(0, 1, (3,3))
print("\n A two dimensional array:\n{}".format(two_dimensional_array) )
A two dimensional array:
[[ 0.95993043 -0.11518909 0.43617329]
[ 0.79277265 -0.40259163 0.28162559]
[-0.42138997 1.33889885 0.21670544]]
# Select the first two indices of each dimension from a 2-dimensional array
two_dimensional_array[0:2, 0:2]
array([[ 0.95993043, -0.11518909],
[ 0.79277265, -0.40259163]])
A single index can also be specified to select a single element from the array.
# Select the single value from the center of this 3x3 array
two_dimensional_array[1,1]
-0.4025916292902783